Characterization of Parabolas and their Graphs
Summary:
In this class, we will review the characterization of parabolas based on their general and canonical forms, explaining how to identify key elements such as the vertex, focus, directrix, axis of symmetry, and possible intersections with the x-axis.
Learning Objectives:
By the end of this class, students will be able to:
- Calculate the position of the vertex, focus, and directrix of the parabola from its general and canonical forms.
- Transform the canonical equation into the general form to extract geometric information.
- Sketch the graph of the parabola using the obtained information.
CONTENTS INDEX
General and Canonical Forms of Parabolas
Characterization of Parabolas from the General Equation
Characterization of Parabolas from the Canonical Equation
Automatic Characterization with Excel
General and Canonical Forms of Parabolas
In the previous class, we saw that parabolas can be expressed algebraically through the general equation of parabolas as follows.
(x-x_0)^2 =4f(y-y_0)
Where the pair (x_0,y_0) represents the position of the vertex and f is the focal distance. If f \gt 0, the focus is at a distance f above the vertex, and if f \lt 0, the focus is at a distance f below the vertex.
We have also seen that the equation of parabolas in its canonical form is equivalent to a second-degree polynomial.
y(x) = ax^2 + bx + c, with a \neq 0
Characterizing a parabola consists of revealing the following information:
- The coordinates of the vertex
- The coordinates of the focus
- The equation of the directrix
- The equation of the axis of symmetry
- The intersections with the x-axis (if they exist)
- Finally, constructing a sketch of the graph using the collected information.
Characterization of Parabolas from the General Equation
If you have the parabola described through the general equation, then you already have almost all the information necessary to complete the characterization, only the intersections with the x-axis will require additional analysis.
(x-x_0)^2 =4f(y-y_0)
From this, you already have:
- Vertex: The point with coordinates (x_0,y_0)
- Focal position: At f units above the vertex
- Focus: The point with coordinates (x_0,y_0 + f)
- Directrix: The line with the equation y= y_0 - f
- Axis of symmetry: The line with the equation x= x_0
To find the intersections with the x-axis, you will need to convert the general equation to its canonical form, set the resulting quadratic polynomial equal to zero. If there are solutions, these will be the intersections with the x-axis.
Characterization of Parabolas from the Canonical Equation
When the equation of the parabola is presented in its canonical form, you have two options: 1) Characterize by transforming into the general equation, or 2) Use the symmetry and the intersections with the x-axis. Both methods have their merits. The second is generally faster, but parabolas do not always intersect the x-axis, the first is more laborious, but as we will see later, it is easy to automate. We will examine both alternatives so you can choose according to your preferences and needs which path to take.
Transforming into the General Equation
The transformation to the general form is done through the following reasoning, where a,b,c\in\mathbb{R} and a\neq 0.
| (1) | y=ax^2 + bx + c | ; Canonical equation of parabolas |
| y=a\left[x^2 + \dfrac{b}{a}x + \dfrac{c}{a}\right] | ; Factoring by a | |
| y=a\left[ \left(x + \dfrac{b}{2a}\right)^2 - \dfrac{b^2}{4a^2} + \dfrac{c}{a}\right] | ; Because \left(x + \dfrac{b}{2a}\right)^2 = x^2 + \dfrac{b}{a}x + \dfrac{b^2}{4a^2} | |
| y=a\left[ \left(x + \dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a^2} \right] | ||
| y=a \left(x + \dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a} | ||
| y=a \left(x + \dfrac{b}{2a}\right)^2 + \left(c - \dfrac{b^2}{4a}\right) | ||
| \left[x - \left(- \dfrac{b}{2a}\right)\right]^2 = \dfrac{1}{a} \left[y - \left(c - \dfrac{b^2}{4a}\right)\right] | ||
| \left[x - \left( -\dfrac{b}{2a}\right)\right]^2 = 4\left(\dfrac{1}{4a}\right) \left[y - \left(c - \dfrac{b^2}{4a}\right)\right] | ; General form of parabolas |
From this, we can extract all the information we had from the general equation by relating its parameters with those of the canonical equation, thus we have:
- Vertex: The point with coordinates (x_0,y_0) = \left(-\dfrac{b}{2a}, c -\dfrac{b^2}{4a} \right)
- Focal position: At f = \dfrac{1}{4a} units above the vertex
- Focus: The point with coordinates (x_0,y_0 + f) = \left(-\dfrac{b}{2a}, c -\dfrac{b^2}{4a} + \dfrac{1}{4a}\right) =\left(-\dfrac{b}{2a}, c +\dfrac{1-b^2}{4a}\right)
- Directrix: The line with the equation y=y_0 - f= c -\dfrac{b^2}{4a} - \dfrac{1}{4a} = c -\dfrac{1 + b^2}{4a}
- Axis of symmetry: The line with the equation x= x_0 = -\dfrac{b}{2a}
And from here, the characterization of parabolas is done as we have already seen using the general equation.
Using Symmetry and x-axis Intersections
When we have the equation of parabolas written in canonical form y=ax^2 + bx+c, we see that it is relatively simple to calculate its intersections with the x-axis, just solve the equation:
ax^2 + bx + c = 0
When this is possible, we get intersections x_1 and x_2 given by:
x_1 = \dfrac{-b + \sqrt{b^2-4ac}}{2a}
x_2 = \dfrac{-b - \sqrt{b^2-4ac}}{2a}
As parabolas are symmetrical, the axis of symmetry will have the equation:
x = x_0 = \dfrac{x_1 + x_2}{2}= -\dfrac{b}{2a}
The axis of symmetry necessarily passes through the vertex of the parabola, whose coordinates are:
(x_0, y_0) = (x_0, y(x_0)) = \left( -\dfrac{b}{2a}, y\left(-\dfrac{b}{2a}\right) \right)
Where:
y_0 = y\left(-\dfrac{b}{2a} \right) = a\left(-\dfrac{b}{2a}\right)^2 + b\left(-\dfrac{b}{2a}\right) + c = \dfrac{b^2}{4a} - \dfrac{b^2}{2a} + c = c - \dfrac{b^2}{4a}
This is how we arrive at the coordinates of the vertex that we already knew by other means:
(x_0, y_0) = \left( -\dfrac{b}{2a},c - \dfrac{b^2}{4a} \right)
The focal position is, as we already saw f=\dfrac{1}{4a}, and from this, we can now calculate the position of the directrix, the focus, and all the information we already had from the general equation.
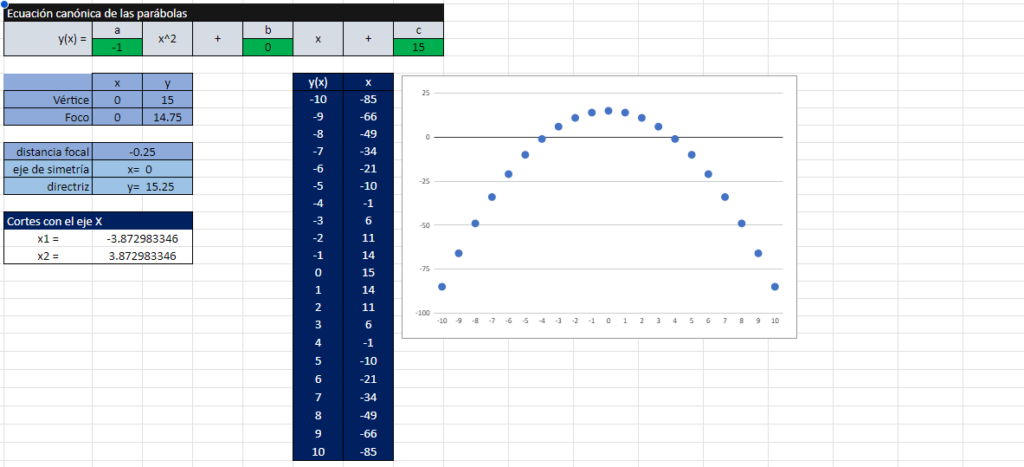
Automatic Characterization with Excel
Having made all these reasonings, it is now very easy to automate the characterization of any parabola using Excel. You can find an example here.