Como calcular a distribuição normal usando a tabela?
Resumo
Nesta aula, abordaremos o tema da distribuição normal, uma das distribuições contínuas de probabilidade mais comuns. Analisaremos como uma variável aleatória X com parâmetros μ e σ pode seguir uma distribuição normal e como essa distribuição pode ser padronizada por meio de uma substituição na integral. No entanto, notaremos que, apesar da simplificação através da padronização, o cálculo analítico da integral continua sendo um desafio, pois não existem expressões algébricas que permitam expressar seu resultado. Para superar esse problema, apresentaremos uma tabela da distribuição normal padrão construída no Excel, que oferece aproximações numéricas aos valores da função. Explicaremos detalhadamente como usar a tabela, incluindo a interpretação das probabilidades acumuladas como áreas sob a curva. Finalmente, a aula conclui com uma série de exercícios práticos focados no cálculo das probabilidades e estimativas usando a tabela da distribuição normal e o conceito de distribuição normal padrão.
OBJETIVOS DE APRENDIZAGEM:
Ao final desta aula, o aluno será capaz de:
- Demonstrar a relação entre a distribuição normal padrão e a distribuição normal com parâmetros \mu e \sigma estabelecidos, por meio de uma substituição integral.
- Resolver problemas práticos usando a tabela de distribuição normal padrão.
- Construir e usar uma tabela de distribuição normal padrão usando Excel.
ÍNDICE DE CONTEÚDOS:
O problema e a solução da distribuição normal
Como uso esta tabela?
Exercícios
O problema e a solução da distribuição normal
Uma das distribuições contínuas de probabilidade mais utilizadas é a distribuição normal. Uma variável aleatória X tem distribuição normal com parâmetros \mu,\sigma se satisfaz que
\displaystyle P(X\leq x) =\Phi_{\mu,\sigma}(x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{1}{2} \left(\frac{t-\mu}{\sigma}\right)^2}dt
e também vimos que essa distribuição pode ser “padronizada” se fizermos na integral uma substituição da forma \displaystyle z= \frac{t-\mu}{\sigma}, obtendo:
\displaystyle \Phi_{\mu,\sigma}(x) = \int_{-\infty}^{\frac{x-\mu}{\sigma}} \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2} }dt = \Phi_{0,1}\left(\frac{x-\mu}{\sigma} \right)
Embora este processo de padronização simplifique a integral, ainda não é suficiente para nos permitir calcular uma única probabilidade para esta distribuição. Acontece que avaliar esta integral de forma analítica não é algo que possamos realizar; na verdade, não existem expressões algébricas que permitam expressar o resultado destas integrais e isso nos coloca em dificuldades. No entanto, se tivermos aproximações numéricas para alguns valores da função de distribuição normal padrão, já podemos começar a fazer algumas estimativas. Esses valores estão resumidos nesta tabela para a distribuição normal padrão que construí no Excel para você >:D
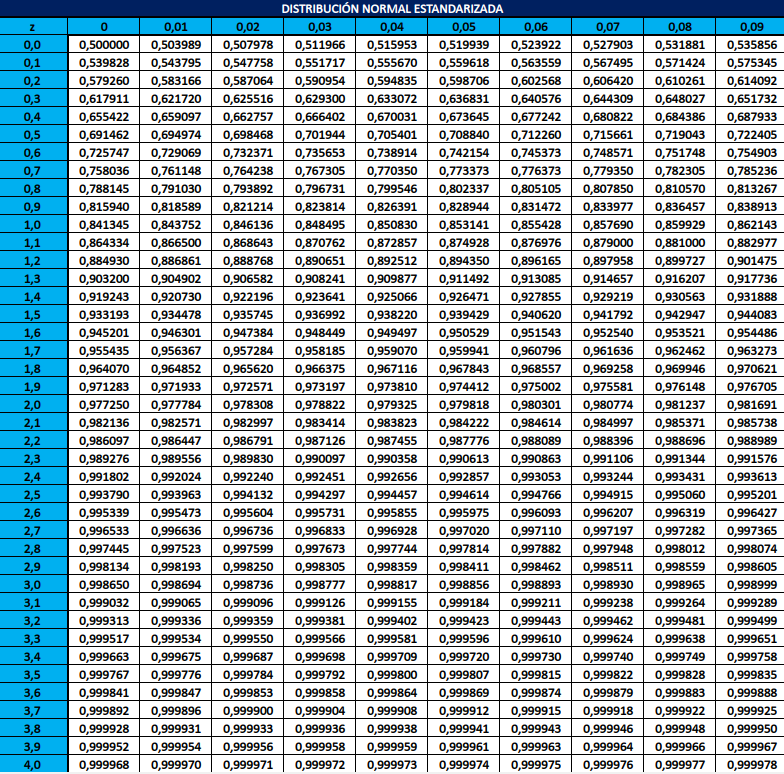
Você pode baixar esta tabela em formato Excel no seguinte link. Recomendo revisar este arquivo porque assim você aprenderá a montar sua própria tabela caso não encontre uma 🙂
Como uso esta tabela?
Para usar esta tabela sem dificuldade você deve lembrar que, além de indicar uma probabilidade acumulada, esta representa uma área sob a curva (da função de densidade). Isso pode ser visto representado na figura a seguir:
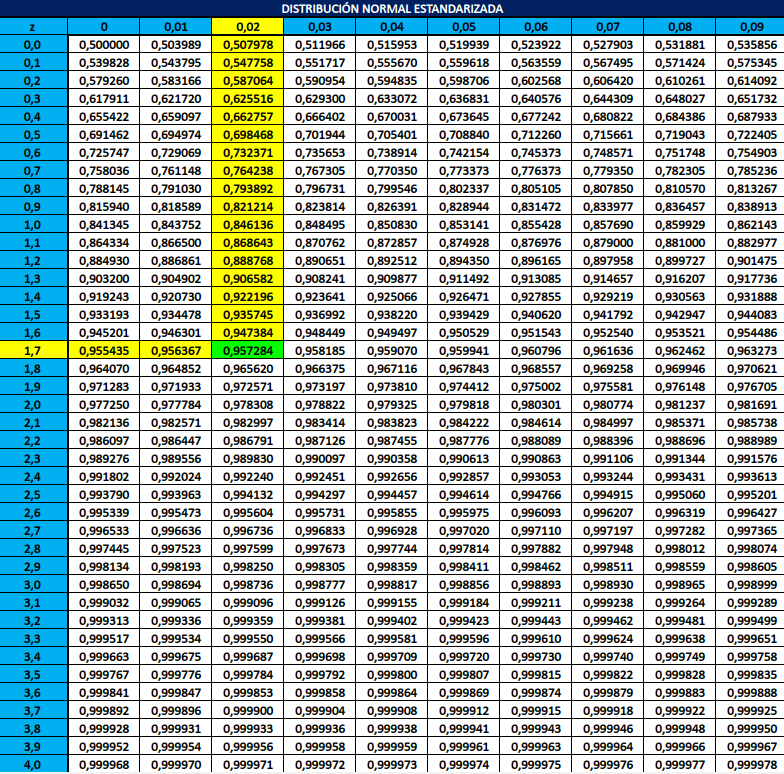
Compreendido isso, o próximo passo é explicar o uso em si da tabela. O que vemos aqui é que o valor z em que vamos avaliar a função \Phi_{0,1}(z) aparece separado em duas partes: na coluna, você encontrará sua expansão até o primeiro dígito decimal, e na linha, você encontrará o segundo dígito decimal; de modo que, por exemplo: o número z=1,72 pode ser encontrado como se estivesse formado por “coordenadas”: a vertical é 1,7, e a horizontal 0,02. Finalmente, a aproximação numérica de \Phi_{0,1}(1,72) aparecerá no bloco de coordenadas “1,7” e “0,02”, que mostra um valor de 0,957284.
Exercícios
- Estime o valor de \Phi_{0,1}(2,93)
- Estime o valor de \Phi_{\mu=12,\sigma=3}(11,5)
- Uma variável aleatória X tem distribuição normal N(\mu=37,\sigma=9). Calcule P(35 \lt X \lt 43).
- A quantidade de tomates que apodrecem diariamente na banca de um feirante tem uma média de \mu=50 com um desvio padrão de \sigma=15. Se o feirante leva tomates 3 vezes por semana, estime o número de dias no mês em que mais de 60 tomates irão apodrecer.
- Assumindo que X \sim N(\mu,\sigma) calcule as seguintes probabilidades:
- P(\mu - \sigma \leq X \leq \mu + \sigma)
- P(X \leq \mu - \sigma \vee \mu + \sigma \leq X)
- P(X \leq \mu - n\sigma \vee \mu + n\sigma \leq X)

