सामान्य वितरण की समस्या और समाधान

संभावना के सबसे अधिक उपयोग किए जाने वाले निरंतर वितरणों में से एक है सामान्य वितरण। एक यादृच्छिक चर X में \mu,\sigma मापदंड होते हैं और यह वितरण सामान्य होता है यदि

\displaystyle P(X\leq x) =\Phi_{\mu,\sigma}(x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{1}{2} \left(\frac{t-\mu}{\sigma}\right)^2}dt

और भी हमने देखा है कि इस वितरण को “मानकीकृत” किया जा सकता है अगर हम समाकलन में प्रतिस्थापन करें जैसे कि \displaystyle z= \frac{t-\mu}{\sigma}, और प्राप्त करें:

\displaystyle \Phi_{\mu,\sigma}(x) = \int_{-\infty}^{\frac{x-\mu}{\sigma}} \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2} }dt = \Phi_{0,1}\left(\frac{x-\mu}{\sigma} \right)

हालांकि यह मानकीकरण प्रक्रिया समाकलन को सरल बनाती है, यह हमें इस वितरण के लिए एक भी संभावना की गणना करने की अनुमति नहीं देती है। ऐसा इसलिए है क्योंकि इस समाकलन का विश्लेषणात्मक रूप से मूल्यांकन करना कुछ ऐसा नहीं है जो हम कर सकते हैं; वास्तव में, इन समाकलनों के परिणाम को व्यक्त करने के लिए कोई बीजगणितीय अभिव्यक्तियाँ नहीं हैं और यह हमें कठिनाइयों में डालता है। हालांकि, अगर हमारे पास सामान्य वितरण मानक फ़ंक्शन के कुछ मूल्यों के लिए संख्यात्मक अनुप्रयोग हैं, तो हम कुछ अनुमान लगाना शुरू कर सकते हैं। ये मान इस सामान्य वितरण मानक तालिका में सारांशित किए गए हैं जिसे मैंने आपके लिए Excel में बनाया है >:D

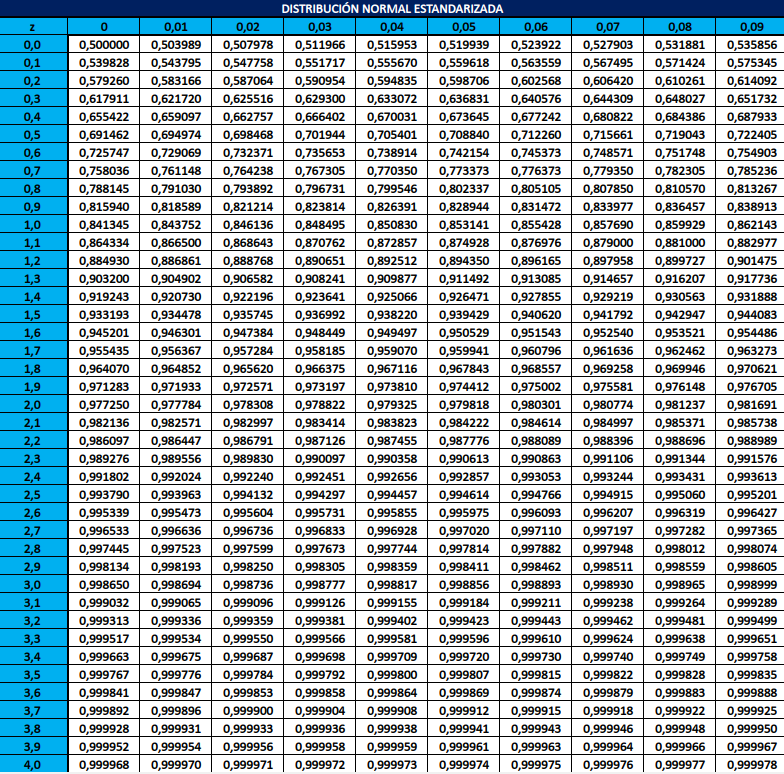
आप इस तालिका को Excel फॉर्मेट में इस लिंक से डाउनलोड कर सकते हैं। मैं आपको उस फ़ाइल की समीक्षा करने की सलाह देता हूं क्योंकि इससे आपको अपना खुद का तालिका बनाने में मदद मिलेगी यदि आपको कोई नहीं मिलता है 🙂

मैं इस तालिका का उपयोग कैसे करूं?

इस तालिका का आसानी से उपयोग करने के लिए आपको याद रखना चाहिए कि, एक संचयी संभावना दिखाने के अलावा, यह एक क्षेत्र को भी दर्शाता है (घनत्व फ़ंक्शन का)। हम इसे निम्नलिखित चित्र में देख सकते हैं:

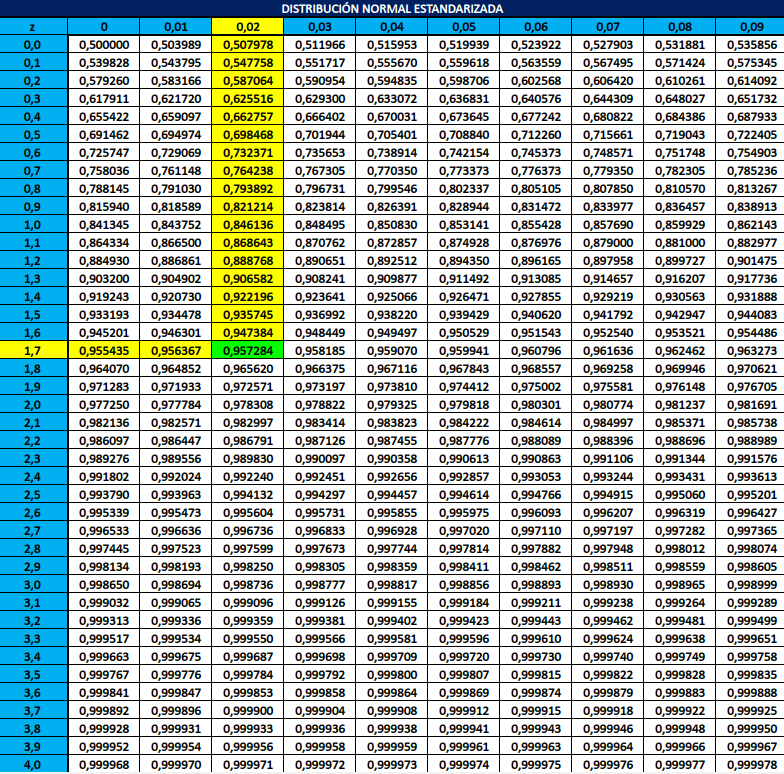
यह समझने के बाद, अगला कदम तालिका के उपयोग की व्याख्या करना है। यहाँ जो हम देखते हैं वह यह है कि वह मान z जिसमें हम \Phi_{0,1}(z) का मूल्यांकन करेंगे, दो भागों में विभाजित दिखाई देता है: कॉलम में आपको पहला दशमलव अंक तक इसका विस्तार मिलेगा, और पंक्ति में आपको दूसरा दशमलव अंक मिलेगा; उदाहरण के लिए: संख्या z=1,72 को “निर्देशांक” के रूप में पाया जा सकता है: लंबवत 1,7, और क्षैतिज 0,02. अंततः, \Phi_{0,1}(1,72) की संख्यात्मक सन्निकटन “1,7” और “0,02” निर्देशांक ब्लॉक में दिखाई देगी, जिसमें 0,957284. का मान प्रदर्शित होगा।

अभ्यास

1. \Phi_{0,1}(2,93) का मान अनुमानित करें।
2. \Phi_{\mu=12,\sigma=3}(11,5) का मान अनुमानित करें।
3. एक यादृच्छिक चर X में N(\mu=37,\sigma=9). वितरण है। P(35 \lt X \lt 43). की गणना करें।
4. एक फेरीवाले के स्टॉल में प्रतिदिन सड़ने वाले टमाटरों की संख्या का औसत \mu=50 होता है और मानक विचलन \sigma=15. यदि फेरीवाला सप्ताह में 3 बार टमाटर लाता है, तो उस महीने के दौरान उन दिनों की संख्या का अनुमान लगाएं जब 60 से अधिक टमाटर सड़ जाएंगे।
5. मान लीजिए कि X \sim N(\mu,\sigma), निम्नलिखित संभावनाओं की गणना करें:
   1. P(\mu - \sigma \leq X \leq \mu + \sigma)
   2. P(X \leq \mu - \sigma \vee \mu + \sigma \leq X)
   3. P(X \leq \mu - n\sigma \vee \mu + n\sigma \leq X)