Introducción

Las lentes delgadas, junto a los espejos, son por lejos los dispositivos ópticos más utilizados. Estas son objetos transparentes cuya superficie es limitada por dos interfaces esféricas y están hechos generalmente de vidrio o plástico.

En una lente delgada, la distancia entre las superficies refractoras es lo suficientemente pequeña como para ser considerada despreciable.

Tipos de lentes

Los lentes, al igual que los espejos, se dividen en dos especies: convergentes y divergentes.

Los puntos F_1 y F_2 son los puntos focales y f es la distancia focal. En una lente fina, las dos longitudes focales son iguales, por eso se representan ambas con la misma letra.

En una lente delgada, la distancia entre las superficies refractoras es lo suficientemente pequeña como para ser considerada despreciable.

Propiedades de las lentes delgadas

Si hacemos geometría con una lente convergente veremos lo siguiente:

Como los triángulos pintados son semejantes, se tendrá que los lados correspondientes son proporcionales

\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}

De forma análoga

\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}

Luego, a partir de (\triangle) y (\star) se tiene:

\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}

Esto último es lo que llamamos relación objeto-imagen para lentes finas.

factor de magnificación m a través de

\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}

Ecuación del fabricante de lentes

Una lente fina, sabemos, se compone de dos interfaces esféricas que separan medios por donde viaja la luz, y ya hemos estudiado lo que ocurre cuando la luz cruza de un medio a otro cruzando interfaces de éste estilo. Por lo tanto, para analizar las lentes finas nos bastará con componer lo que ya revisamos para interfaces individualmente.

En general, una lente fina tiene la siguiente apariencia:

Pero para mayor simpleza, esto se puede separar

Dado que cada caso ya lo hemos analizado (aquí), podemos extraer las siguientes dos ecuaciones:

Para el lado a-b:

\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}

Para el lado b-c:

\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}

En este punto, si hacemos n_a = n_c = n_{aire}\approx 1.0, ocurrirá que s_b = -s_{ab}^\prime; por lo tanto, estas ecuaciones queda escritas de la siguiente forma

\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}

y sumándolas, ahora es posible obtener una sola expresión:

\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}

En este punto es conveniente renombrar las variables en juego, utilizaremos el siguiente cambio de nombres

\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}

de modo que obtendremos una versión más «limpia» de la ecuación que originalmente habíamos obtenido:

\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)

Finalmente, utilizando la relación objeto-imagen para lentes finas se dedujo al principio, se consigue:

\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}

Esto es lo que llamamos Ecuación del Fabricante de Lentes.

Métodos gráficos para lentes delgadas

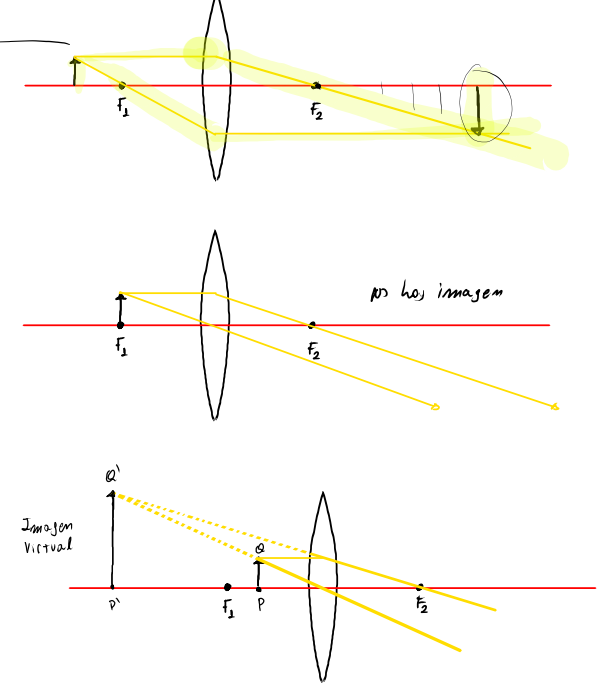
Una herramienta muy útil para corroborar o encontrar sentido a los cálculos que realizamos son los métodos gráficos que se dibujan a continuación; tales métodos son análogos a los utilizados con los espejos.

Estos métodos proporcionan distintos resultados según la posición del objeto frente al lente.

Ejercicios:

1. Se tiene un lente divergente y un haz de rayos paralelos que «se abre» al pasar por el de modo tal que sus proyecciones convergen a un punto situado a 30[cm] del centro del lente. Si se desea usar este lente para obtener una imagen virtual de 1/2 de la altura de un cierto objeto:
   1. Calcule el lugar donde debe estar tal objeto.
   2. Haga un diagrama de rayos para describir la situación.
2. Un objeto de 7[cm] de alto es puesto a 13[cm] a la izquierda de una lente convergente de longitud focal de 5[cm]. Un segundo lente convergente de longitud focal de 2[cm] es puesta a 30[cm] a la derecha del primer lente compartiendo ambos el mismo eje óptico. Encuentre el tamaño y la posición de la imagen generada por los dos lentes combinados.