Introduction

Les lentilles minces, avec les miroirs, sont de loin les dispositifs optiques les plus utilisés. Ce sont des objets transparents dont la surface est limitée par deux interfaces sphériques, généralement fabriqués en verre ou en plastique.

Dans une lentille mince, la distance entre les surfaces réfractantes est suffisamment petite pour être considérée comme négligeable.

Types de lentilles

Les lentilles, comme les miroirs, se divisent en deux types : convergentes et divergentes.

Les points F_1 et F_2 sont les points focaux, et f est la distance focale. Dans une lentille mince, les deux distances focales sont égales, c’est pourquoi elles sont représentées par la même lettre.

Dans une lentille mince, la distance entre les surfaces réfractantes est suffisamment petite pour être considérée comme négligeable.

Propriétés des lentilles minces

Si nous faisons de la géométrie avec une lentille convergente, nous verrons ce qui suit :

Comme les triangles tracés sont similaires, les côtés correspondants seront proportionnels

\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}

De même,

\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}

Puis, à partir de (\triangle) et (\star), on obtient :

\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}

Ce dernier est ce que nous appelons la relation objet-image pour les lentilles minces.

facteur de grossissement m par

\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}

Équation du fabricant de lentilles

Une lentille mince, comme nous le savons, est composée de deux interfaces sphériques qui séparent les milieux à travers lesquels la lumière voyage, et nous avons déjà étudié ce qui se passe lorsque la lumière passe d’un milieu à un autre en traversant ces interfaces. Ainsi, pour analyser les lentilles minces, il suffit de combiner ce que nous avons déjà étudié pour les interfaces individuelles.

En général, une lentille mince a l’apparence suivante :

Mais pour simplifier, cela peut être séparé

Puisque chaque cas a déjà été analysé (ici), nous pouvons en extraire les deux équations suivantes :

Pour le côté a-b :

\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}

Pour le côté b-c :

\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}

À ce stade, si nous faisons n_a = n_c = n_{air}\approx 1.0, il se trouve que s_b = -s_{ab}^\prime; par conséquent, ces équations sont écrites de la manière suivante

\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}

et en les additionnant, il est maintenant possible d’obtenir une seule expression :

\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}

À ce stade, il est pratique de renommer les variables en jeu ; nous utiliserons la dénomination suivante :

\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}

ainsi, nous obtiendrons une version plus « propre » de l’équation que nous avions initialement obtenue :

\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)

Enfin, en utilisant la relation objet-image pour les lentilles minces déduite au début, on obtient :

\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}

C’est ce que nous appelons l’équation du fabricant de lentilles.

Méthodes graphiques pour les lentilles minces

Un outil très utile pour vérifier ou comprendre les calculs que nous effectuons sont les méthodes graphiques illustrées ci-dessous ; ces méthodes sont analogues à celles utilisées avec les miroirs.

Ces méthodes donnent des résultats différents selon la position de l’objet devant la lentille.

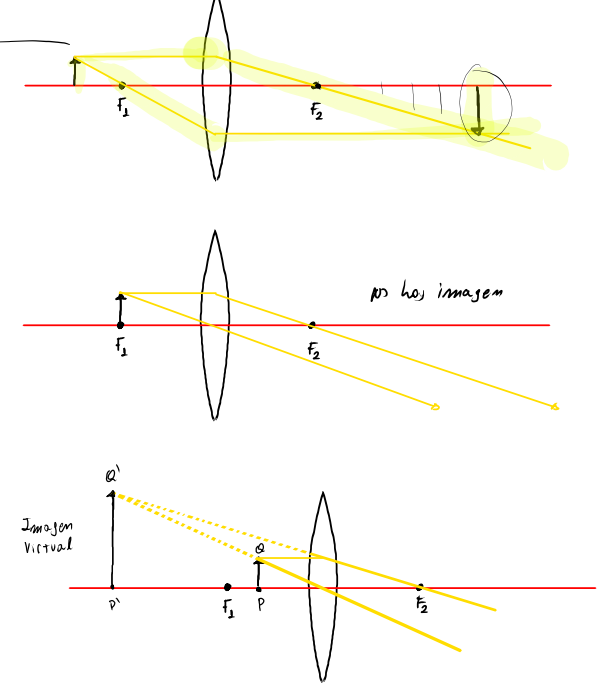
Exercices :

1. On dispose d’une lentille divergente et d’un faisceau de rayons parallèles qui se « diverge » en passant à travers elle de manière à ce que leurs projections convergent en un point situé à 30[cm] du centre de la lentille. Si vous souhaitez utiliser cette lentille pour obtenir une image virtuelle d’une hauteur égale à la moitié de celle d’un certain objet :
   1. Calculez où doit se trouver cet objet.
   2. Faites un diagramme des rayons pour décrire la situation.
2. Un objet de 7[cm] de hauteur est placé à 13[cm] à gauche d’une lentille convergente de distance focale de 5[cm]. Une deuxième lentille convergente de distance focale de 2[cm] est placée à 30[cm] à droite de la première lentille, partageant les deux le même axe optique. Trouvez la taille et la position de l’image formée par les deux lentilles combinées.