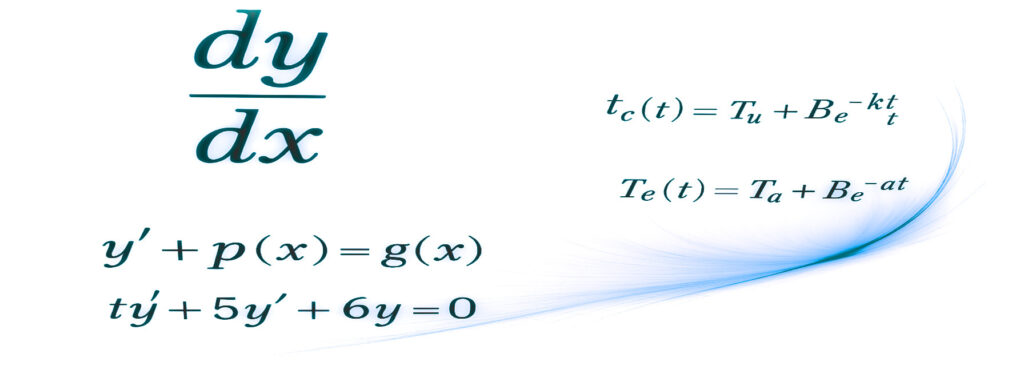Introduction to Ordinary Differential Equations
This class offers a detailed exploration of the fundamental ideas that govern these equations and their applications in various fields. Beginning with an analysis of the nature of constant change in the world around us, basic concepts such as functions, derivatives, and their relationship with continuous and discrete change are presented. The distinction between Partial Differential Equations (PDEs) and Ordinary Differential Equations (ODEs) is introduced, focusing on the study of ODEs. Concepts are illustrated with practical examples such as the cooling of a cup of coffee, Newton’s Laws, and population models. Students will have the opportunity to become familiar with differential equations that govern natural and physical phenomena, discover how they can be mathematically represented, and understand some techniques to study their solutions. This initial knowledge will constitute the foundation for more advanced studies in differential equations and their applications in science and engineering.
Learning Objectives:
By the end of this class, the student will be able to:
- Understand the basic concepts related to differential equations, such as the nature of change, functions, derivatives, and the differences between Partial Differential Equations (PDEs) and Ordinary Differential Equations (ODEs)
INDEX
Differential Equations and the Nature of Things
The Constant Change
Functions, Derivatives, and Their Changes
ODEs and PDEs
Examples of Ordinary Differential Equations
The Cooling of a Cup of Coffee
Newton’s Laws
Population Model
Differential Equations and the Nature of Things
The Constant Change
In nature, everything is in constant change. Even things that seem to never change, like the brightness of the Sun, vary if observed on the appropriate time scale. Everything changes: the brightness of stars, the temperature of coffee in a cup, the position of an object, and the size of a population are some examples, and these rates of change are generally related to the state of what is changing while that change occurs.
An intuitive way to understand change is to observe how things change over time. The change that occurs with respect to time is what we call evolution, and everything we can observe is in continuous evolution. But evolution is not the only form of change; for example, although our height above sea level may vary over time, it is more likely to change depending on our position (or geographic coordinates).
Functions, Derivatives, and Their Changes
In more general terms, a function of several variables f(x_1,x_2, \cdots, x_n) can vary if any of its variables change, and that change can be continuous or discrete. For a function of several variables, continuous change can be studied through partial derivatives:
\displaystyle \frac{\partial f(x_1, \cdots, x_n)}{\partial x_1} = \lim_{\Delta x_1 \to 0} \frac{ f(x_1 + \Delta x_1, \cdots, x_n) - f(x_1, \cdots, x_n)}{\Delta x_1}
If the function is of a single variable, the ordinary derivative is used:
\displaystyle \frac{df(x)}{dx} = \lim_{\Delta x \to 0} \frac{ f(x + \Delta x) - f(x)}{\Delta x}
If the change is discrete instead of continuous, the calculation of the limit that appears in the derivatives is simply omitted.
ODEs and PDEs
An equation involving a function and its different derivatives is known as a Differential Equation. If these derivatives are partial or ordinary, they are called respectively Partial Differential Equations (PDEs) or Ordinary Differential Equations (ODEs). At this point, we will focus on the study of ordinary differential equations and review some examples where they appear.
Examples of Ordinary Differential Equations
The Cooling of a Cup of Coffee
The cooling rate of a cup of coffee is proportional to the temperature difference between the environment and the coffee. If the air temperature, T_a, is constant and the temperature of the coffee is a function of time T_c=T_c(t), we can find a differential equation that will allow us to determine the temperature of the coffee at any moment. Initially, we have:
\displaystyle \frac{dT_c(t)}{dt} = -\alpha^2(T_c(t) - T_a)
Where \alpha is a proportionality constant, T_a \lt T_c(t), and the negative sign indicates that the temperature of the coffee is decreasing. Later, we will see that this equation has a solution of the form:
T_c(t) = T_a + Be^{-\alpha^2 t}
Where B is a constant to be determined.
Newton’s Laws
Newton’s Second Law is, essentially, an ordinary differential equation, since in the expression F=ma (force equals mass times acceleration), the acceleration, a=d^2x(t)/dt^2,, is the second time derivative of the object’s position. Through this law, we can find relationships that describe the motion of bodies, which are actually differential equations. A simple example is the study of springs: if we have a spring attached to a fixed wall on one side and to a mass on the other at equilibrium position, and then we displace the mass a distance x from that position, according to Hooke’s Law the mass will feel a restoring force F=-kx. Then, by Newton’s second law, we have:
\displaystyle -kx(t) = m\frac{d^2x(t)}{dt^2}
Later, we will see that its solution is of the form:
\displaystyle x(t) = A\sin\left(\sqrt{\frac{k}{m}}t + \phi \right)
Where A and \phi are constants that will be determined by the initial conditions of the problem.
Population Model
The growth rate per individual of a population is equal to the difference between the birth and death rates, that is:
\displaystyle \frac{1}{x(t)} \frac{dx(t)}{dt} = N - M
If the birth rate N remains constant over time and deaths are proportional to the population, that is M=\alpha^2 x(t),, then the previous equation takes the form:
\displaystyle \frac{dx(t)}{dt} = x(t) (N - \alpha^2 x(t))
This is known as the “Logistic Equation of Populations”. From this equation, a generalization can be constructed for many populations x_1(t), x_2(t), \cdots, x_n(t) that compete with each other to exist as follows:
\displaystyle \frac{dx_i(t)}{dt} = x_i(t) \left(N_i - \displaystyle \sum_{j=1}^n\alpha^2_{ij} x_j(t) \right)
With i\in\{1,\cdots, n\}. This is what is known as the Lotka-Volterra Equations.
Conclusion
Throughout this introduction to Ordinary Differential Equations, we have explored how mathematics can precisely and elegantly capture the changes that occur in the natural world. From the cooling of a cup of coffee to the motion of a spring or the growth of a population, ODEs allow us to translate complex dynamics into understandable and analyzable mathematical relationships.
Understanding the structure and meaning of these equations opens the door to multiple disciplines, such as physics, biology, economics, and engineering. This class lays the necessary conceptual foundations to continue with more advanced studies, where solution techniques, qualitative analysis, and numerical methods will be explored in greater depth. Most importantly, however, is having developed an initial intuition about how the language of change —differential equations— allows us to describe, understand, and predict the behavior of dynamic systems.
In the following classes, we will continue developing more powerful tools and applying them to new contexts. Differential equations not only offer us a way to analyze reality, but also to imagine how it could evolve under different conditions.