Dünne Linsen: Alles über ihre Eigenschaften und Berechnungen

Zusammenfassung:
Diese Vorlesung führt in die dünnen Linsen ein, erklärt ihre Typen (konvergente und divergente), ihre optischen Eigenschaften und die Objekt-Bild-Beziehung. Es werden grafische Methoden vorgestellt und die Linsengleichung des Herstellers hergeleitet, um ihr Funktionieren zu verstehen. Ziel ist es, ein grundlegendes Verständnis für dünne Linsen und ihre Anwendung in der Optik zu vermitteln, ergänzt durch praktische Übungen.

Lernziele:
Am Ende dieser Vorlesung wird der Studierende in der Lage sein:

• Die optischen Eigenschaften dünner Linsen zu verstehen, einschließlich Brennweite und Brennpunkte.
• Die verschiedenen Typen dünner Linsen, wie konvergente und divergente Linsen, sowie deren Anwendungen zu identifizieren.
• Die Objekt-Bild-Beziehung anzuwenden, um optische Probleme mit dünnen Linsen zu lösen.
• Zu analysieren, wie sphärische Flächen in dünnen Linsen die Lichtbrechung beeinflussen.
• Die Linsengleichung des Herstellers zu erklären und ihre Relevanz bei der Herstellung optischer Linsen darzustellen.
• Grafische Methoden zu verwenden, um Bild- und Objektpositionen in dünnen Linsen zu bestimmen.
• Die Vergrößerung von durch dünne Linsen erzeugten Bildern zu berechnen.
• Formeln herzuleiten aus der Geometrie dünner Linsen, um optische Probleme zu lösen.

INHALTSVERZEICHNIS
Einführung
Linsentypen
Eigenschaften dünner Linsen
Linsengleichung des Herstellers
Grafische Methoden für dünne Linsen
Übungen

Einführung

Dünne Linsen sind zusammen mit Spiegeln bei weitem die am häufigsten verwendeten optischen Geräte. Es handelt sich um transparente Objekte, deren Oberfläche durch zwei sphärische Grenzflächen begrenzt ist und die in der Regel aus Glas oder Kunststoff bestehen.

Bei einer dünnen Linse ist der Abstand zwischen den brechenden Flächen so klein, dass er als vernachlässigbar angesehen werden kann.

Linsentypen

Linsen, ebenso wie Spiegel, werden in zwei Arten unterteilt: konvergente und divergente.

 

Die Punkte F_1 und F_2 sind die Brennpunkte und f ist die Brennweite. Bei einer dünnen Linse sind die beiden Brennweiten gleich, weshalb beide mit demselben Buchstaben dargestellt werden.

Bei einer dünnen Linse ist der Abstand zwischen den brechenden Flächen so klein, dass er als vernachlässigbar angesehen werden kann.

Eigenschaften dünner Linsen

Wenn wir mit einer Linse Geometrie betreiben, die konvergent ist, sehen wir Folgendes:

 

Da die gezeichneten Dreiecke ähnlich sind, gilt, dass die entsprechenden Seiten proportional sind.

\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}

In ähnlicher Weise

\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}

Dann ergibt sich aus (\triangle) und (\star):

\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}

Dies ist das, was wir die Objekt-Bild-Beziehung für dünne Linsen nennen.

Analog zu den Spiegeln ist es möglich, den Vergrößerungsfaktor m zu definieren durch

\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}

Linsengleichung des Herstellers

Eine dünne Linse besteht, wie wir wissen, aus zwei sphärischen Grenzflächen, die Medien trennen, durch die das Licht verläuft. Wir haben bereits untersucht, was geschieht, wenn Licht von einem Medium in ein anderes über eine solche Grenzfläche übertritt. Daher genügt es zur Analyse dünner Linsen, das, was wir bereits für einzelne Grenzflächen betrachtet haben, zusammenzusetzen.

Im Allgemeinen hat eine dünne Linse folgendes Aussehen:

Zur Vereinfachung kann dies jedoch getrennt werden:

Da jeder Fall bereits analysiert wurde (hier), können wir die folgenden beiden Gleichungen ableiten:

Für die Seite a-b:

\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}

Für die Seite b-c:

\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}

An diesem Punkt, wenn wir n_a = n_c = n_{Luft}\approx 1.0, setzen, tritt der Fall ein, dass s_b = -s_{ab}^\prime; daher können diese Gleichungen in folgender Form geschrieben werden:

\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}

Und wenn man sie addiert, ist es nun möglich, einen einzigen Ausdruck zu erhalten:

\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}

An diesem Punkt ist es zweckmäßig, die beteiligten Variablen umzubenennen. Wir verwenden die folgende Umbenennung:

\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}

so dass wir eine „sauberere“ Version der ursprünglich erhaltenen Gleichung erhalten:

\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)

Schließlich erhält man unter Verwendung der zuvor hergeleiteten Objekt-Bild-Beziehung für dünne Linsen:

\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}

Dies ist das, was wir die Linsengleichung des Herstellers nennen.

Grafische Methoden für dünne Linsen

Ein sehr nützliches Werkzeug zur Überprüfung oder um den Berechnungen, die wir durchführen, Bedeutung zu verleihen, sind die grafischen Methoden, die im Folgenden dargestellt werden; solche Methoden sind analog zu den bei Spiegeln verwendeten.

Diese Methoden liefern unterschiedliche Ergebnisse je nach Position des Objekts vor der Linse.

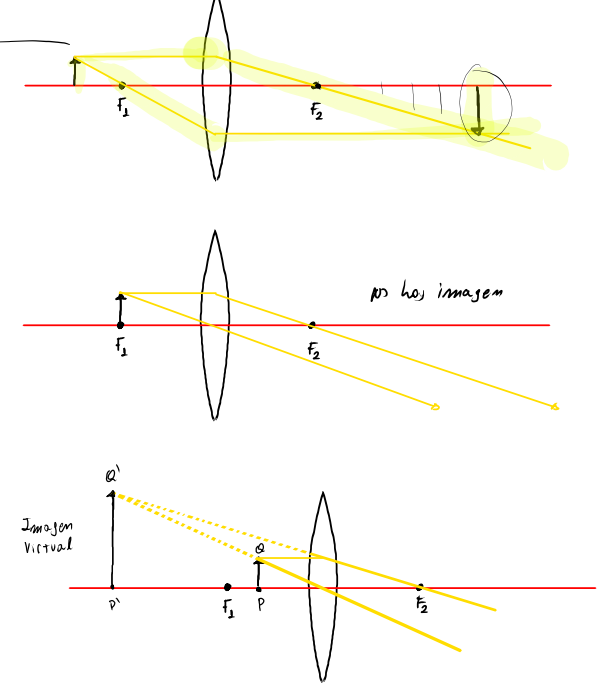
Übungen:

1. Es liegt eine divergente Linse und ein paralleles Strahlenbündel vor, das sich beim Durchgang durch die Linse „öffnet“, so dass seine Projektionen in einem Punkt in 30[cm] Entfernung vom Zentrum der Linse konvergieren. Wenn diese Linse verwendet werden soll, um ein virtuelles Bild mit halber Höhe eines bestimmten Objekts zu erzeugen:
   1. Berechnen Sie den Ort, an dem sich dieses Objekt befinden muss.
   2. Erstellen Sie ein Strahlendiagramm zur Beschreibung der Situation.
2. Ein 7[cm] hohes Objekt wird 13[cm] links von einer konvergenten Linse mit einer Brennweite von 5[cm] platziert. Eine zweite konvergente Linse mit einer Brennweite von 2[cm] wird 30[cm] rechts von der ersten Linse aufgestellt, wobei beide die gleiche optische Achse teilen. Bestimmen Sie die Größe und die Position des Bildes, das durch die beiden kombinierten Linsen erzeugt wird.