薄いレンズ:その特性と計算について
概要:
この授業では薄いレンズを紹介し、その種類(収束レンズと発散レンズ)、光学的特性、物体と像の関係を説明します。図解的な方法を提示し、レンズメーカーの公式を導出してその仕組みを理解します。目的は、薄いレンズとその光学への応用についての基礎的な理解を提供し、実践的な演習で補完することです。
学習目標:
この授業を終えると、学生は次のことができるようになります。
- 理解する 薄いレンズの光学的特性、焦点距離や焦点を含む。
- 識別する 薄いレンズの異なる種類、例えば収束レンズや発散レンズ、およびその応用。
- 適用する 物体と像の関係を用いて、薄いレンズを利用した光学問題を解決する。
- 分析する 薄いレンズにおける球面が光の屈折にどのように影響するか。
- 説明する レンズメーカーの公式と、その光学レンズ製造における重要性。
- 利用する 図解的な方法を用いて、薄いレンズにおける像と物体の位置を決定する。
- 計算する 薄いレンズによって生成される像の倍率。
- 導出する 薄いレンズの幾何学から光学問題を解決するための公式。
内容目次
序論
レンズの種類
薄いレンズの特性
レンズメーカーの公式
薄いレンズの図解的方法
演習
序論
薄いレンズは、 鏡と並んで、最も広く使用されている光学デバイスです。これは透明な物体であり、その表面は2つの球面界面によって制限され、一般的にガラスやプラスチックで作られています。

薄いレンズでは、屈折面間の距離は十分に小さいため、無視できると見なされます。
レンズの種類
レンズは鏡と同様に、 2つの種類に分類されます:収束レンズと発散レンズ。


点 F_1 と F_2 は焦点であり、f は焦点距離です。薄いレンズでは、2つの焦点距離は等しいため、同じ記号で表されます。
薄いレンズにおいては、屈折面間の距離は十分に小さいため、無視できると見なされます。
薄いレンズの特性
収束レンズで幾何学的に考察すると、 次のことが分かります。

塗られた三角形は相似であるため、対応する辺は比例関係にあります。
\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}
同様にして
\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}
その後、(\triangle) と (\star) から次が得られます。
\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}
これが薄いレンズにおける物体と像の関係と呼ばれるものです。
鏡と同様に、倍率 m を次のように定義することができます。
\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}
レンズメーカーの公式
薄いレンズは、2つの球面界面から構成されていることが分かっています。 それらは光が通過する媒体を分けており、すでに光がこのような界面を通過するときに何が起こるかを学びました。したがって、薄いレンズを解析するためには、すでに個別の界面で確認したものを組み合わせれば十分です。
一般に、薄いレンズは次のような外観を持ちます。

しかし、より単純化のために、これは分けて考えることができます。

各ケースはすでに解析済みであるため、次の2つの方程式を導き出すことができます。
a-b 側の場合:
\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}
b-c 側の場合:
\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}
ここで、n_a = n_c = n_{aire}\approx 1.0, とすると、s_b = -s_{ab}^\prime; となります。したがって、これらの方程式は次のように書き換えられます。
\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}
これらを加えることで、1つの式を得ることができます。
\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}
ここで、変数の名称を次のように置き換えると便利です。
\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}
このようにして、もともと導かれた方程式をより「整理された」形で表すことができます。
\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)
最後に、最初に導出した薄いレンズにおける物体と像の関係を用いると、次が得られます。
\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}
これがレンズメーカーの公式と呼ばれるものです。
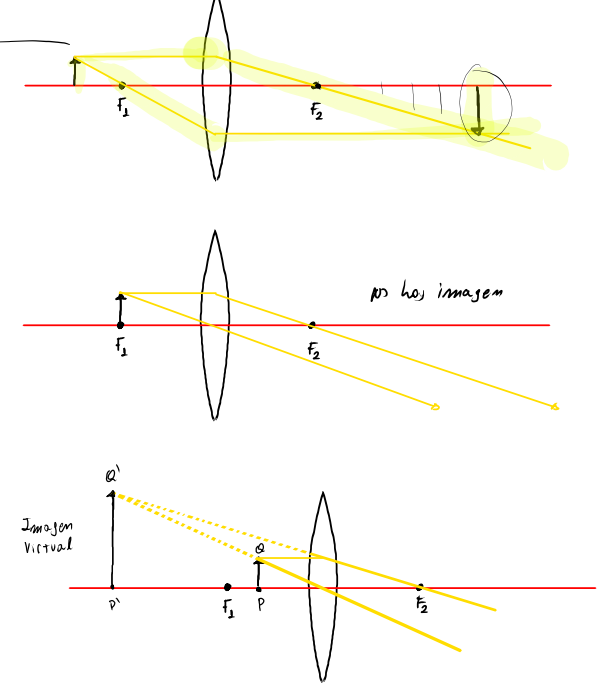
薄いレンズの図解的方法
計算を確認したり、理解を深めるための非常に有用な手段 が、以下に示す図解的方法です。これらの方法は、鏡で用いられるものと類似しています。

これらの方法は、物体の位置によって異なる結果をもたらします。
演習:
- 発散レンズがあり、平行光線の束が通過するときに「開き」、その延長線がレンズの中心から30[cm]の点に収束するとします。このレンズを用いて、ある物体の高さの1/2の虚像を得たいとします。
- その物体を置くべき位置を計算しなさい。
- 状況を説明するための光線図を描きなさい。
- 高さ7[cm]の物体が収束レンズの左側13[cm]の位置に置かれています。このレンズの焦点距離は5[cm]です。焦点距離2[cm]の第2の収束レンズが、最初のレンズの右側30[cm]の位置に、同じ光軸を共有するように配置されています。2枚のレンズを組み合わせたときに生成される像の大きさと位置を求めなさい。

