薄透镜:关于其特性和计算的一切
摘要:
本课介绍了薄透镜,解释了其类型(会聚和发散)、光学特性和物体-图像关系。介绍了图解方法,并推导了透镜制造方程以理解其工作原理。目标是提供对薄透镜及其在光学中应用的基本理解,并辅以实际练习。
学习目标:
在本课结束时,学生将能够:
- 理解薄透镜的光学特性,包括焦距和焦点。
- 识别薄透镜的不同类型,如会聚透镜和发散透镜及其应用。
- 应用物体-图像关系解决使用薄透镜的光学问题。
- 分析薄透镜中的球面如何影响光的折射。
- 解释透镜制造方程及其在光学透镜制造中的重要性。
- 使用图解方法确定薄透镜中的物体和图像位置。
- 计算薄透镜产生的图像放大率。
- 推导薄透镜几何学中的公式来解决光学问题。
介绍
薄透镜, 与镜子一样,是最广泛使用的光学设备。它们是由两个球面界面限制的透明物体,通常由玻璃或塑料制成。

在薄透镜中,折射面之间的距离小到可以忽略不计。
透镜的类型
透镜,像镜子一样,分为两种类型:会聚透镜和发散透镜。
 薄透镜 会聚
薄透镜 会聚  薄透镜 发散
薄透镜 发散
点 F_1 和 F_2 是焦点,f 是 焦距。 在薄透镜中,两个焦距相等,所以用相同的字母表示。
在薄透镜中,折射面之间的距离小到可以忽略不计。
薄透镜的特性
如果我们用会聚透镜做几何,我们将看到以下内容:

由于所绘三角形相似,对应的边将成比例
\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}
同样,
\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}
然后,从 (\triangle) 和 (\star) 得出:
\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}
以上就是我们所说的 薄透镜的物体-图像关系。
放大因子 m 通过
\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}
透镜制造方程
如我们所知,薄透镜由两个球面界面组成,它们分隔了光线通过的介质,我们已经研究了当光线穿过这种界面时会发生什么。因此,分析薄透镜时,我们只需组合之前针对单个界面所学的内容。
通常,薄透镜的外观如下:

但为了简化,这可以分开

由于我们已经分析了每种情况(这里),我们可以得出以下两个方程:
对于a-b边:
\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}
对于b-c边:
\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}
此时,如果我们设置 n_a = n_c = n_{air}\approx 1.0, 那么 s_b = -s_{ab}^\prime; 因此,这些方程写成以下形式
\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}
将它们相加,现在可以得到一个表达式:
\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}
此时,方便重新命名涉及的变量;我们将使用以下命名规则
\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}
因此,我们将获得一个更“简洁”的版本的方程:
\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)
最后,利用一开始推导出的薄透镜的物体-图像关系,得到:
\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}
这就是我们所说的 透镜制造方程。
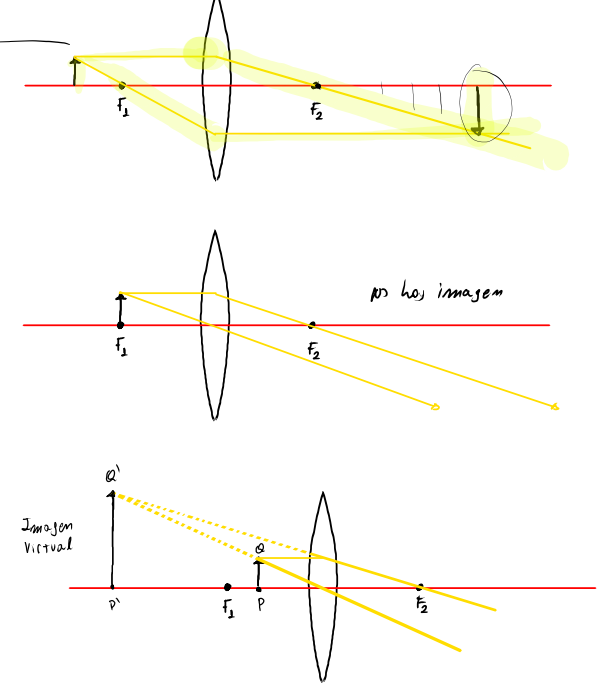
薄透镜的图解方法
验证或理解我们所做的计算的一个非常有用的工具是下面绘制的图解方法;这些方法与镜子使用的方法类似。

根据物体在透镜前的位置,这些方法提供不同的结果。
练习:
- 一个发散透镜和一束平行光束在通过透镜时“散开”,使其投影会聚到距透镜中心30[cm]的点。如果你想用这个透镜获得一个高度为某物体一半的虚像:
- 计算物体应放置的位置。
- 画出描述这种情况的光线图。
- 一个高7[cm]的物体被放置在距焦距为5[cm]的会聚透镜左边13[cm]处。第二个焦距为2[cm]的会聚透镜被放置在距第一个透镜右边30[cm]处,两个透镜共享同一光轴。找到这两个透镜组合产生的图像的大小和位置。

