Introdução

As lentes delgadas, junto com os espelhos, são de longe os dispositivos ópticos mais utilizados. Estes são objetos transparentes cuja superfície é limitada por duas interfaces esféricas e são geralmente feitos de vidro ou plástico.

Em uma lente delgada, a distância entre as superfícies refrativas é pequena o suficiente para ser considerada desprezível.

Tipos de Lentes

As lentes, assim como os espelhos, são divididas em dois tipos: convergentes e divergentes.

Os pontos F_1 e F_2 são os pontos focais e f é a distância focal. Em uma lente fina, as duas distâncias focais são iguais, por isso são representadas pela mesma letra.

Em uma lente delgada, a distância entre as superfícies refrativas é pequena o suficiente para ser considerada desprezível.

Propriedades das Lentes Delgadas

Se fizermos geometria com uma lente convergente, veremos o seguinte:

Como os triângulos pintados são semelhantes, os lados correspondentes serão proporcionais

\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}

Da mesma forma,

\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}

Então, a partir de (\triangle) e (\star) temos:

\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}

O que acabamos de ver é o que chamamos de relação objeto-imagem para lentes finas.

fator de ampliação m através de

\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}

Equação do Fabricante de Lentes

Uma lente fina, como sabemos, é composta por duas interfaces esféricas que separam os meios pelos quais a luz viaja, e já estudamos o que acontece quando a luz cruza de um meio para outro, atravessando interfaces desse tipo. Portanto, para analisar lentes finas, bastará compor o que já revisamos para interfaces individuais.

Em geral, uma lente fina tem a seguinte aparência:

Mas para simplificar, isso pode ser separado

Já que analisamos cada caso (aqui), podemos extrair as seguintes duas equações:

Para o lado a-b:

\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}

Para o lado b-c:

\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}

Neste ponto, se fizermos n_a = n_c = n_{ar}\approx 1.0, acontecerá que s_b = -s_{ab}^\prime; portanto, essas equações são escritas da seguinte forma

\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}

e somando-as, agora é possível obter uma única expressão:

\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}

Neste ponto, é conveniente renomear as variáveis em jogo; usaremos a seguinte troca de nomes

\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}

de modo que obteremos uma versão mais “limpa” da equação que originalmente havíamos obtido:

\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)

Finalmente, utilizando a relação objeto-imagem para lentes finas que foi deduzida no início, obtém-se:

\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}

Isso é o que chamamos de Equação do Fabricante de Lentes.

Métodos Gráficos para Lentes Delgadas

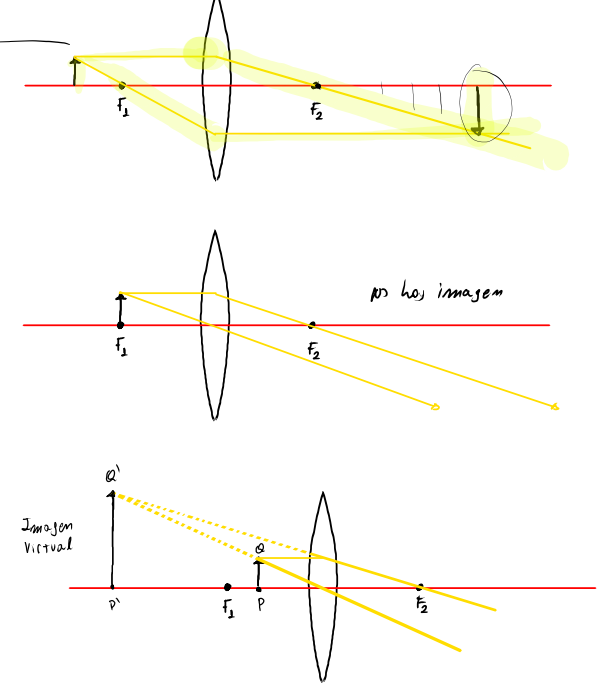
Uma ferramenta muito útil para corroborar ou encontrar sentido nos cálculos que realizamos são os métodos gráficos desenhados abaixo; tais métodos são análogos aos utilizados com espelhos.

Estes métodos fornecem diferentes resultados dependendo da posição do objeto em frente à lente.

Exercícios:

1. Temos uma lente divergente e um feixe de raios paralelos que “se abrem” ao passar por ela, de modo que suas projeções convergem para um ponto situado a 30[cm] do centro da lente. Se você deseja usar esta lente para obter uma imagem virtual de 1/2 da altura de um determinado objeto:
   1. Calcule onde tal objeto deve ser colocado.
   2. Faça um diagrama de raios para descrever a situação.
2. Um objeto de 7[cm] de altura é colocado a 13[cm] à esquerda de uma lente convergente com distância focal de 5[cm]. Uma segunda lente convergente com distância focal de 2[cm] é colocada a 30[cm] à direita da primeira lente, compartilhando ambas o mesmo eixo óptico. Encontre o tamanho e a posição da imagem gerada pelas duas lentes combinadas.