Lens tenuis: Omnia de proprietatibus eius et calculis

Summarium:
Haec lectio lens tenues introducit, explicans earum genera (convergentes et divergentes), proprietates opticas atque relationem obiecti-imaginis. Methodi graphici proponuntur et aequatio fabricantium lentium deducitur ad intellectum functionis earum. Propositum est comprehensionem fundamentalem lentium tenuium earumque applicationem in optica praebere, exercitiis practicis completam.

Proposita Discendi:
hoc cursu absoluto discipulus poterit:

• Intelligere proprietates opticas lentium tenuium, inter distantiam focalem et puncta focalia.
• Identificare varia genera lentium tenuium, ut lentes convergentes et divergentes, earumque applicationes.
• Applicare relationem obiecti-imaginis ad problemata optica solvenda utens lentibus tenuibus.
• Analyzare quomodo superficies sphaericae in lentibus tenuibus refractionem luminis afficiant.
• Explicare aequationem fabricantium lentium eiusque momentum in confectione lentium opticorum.
• Uti methodis graphicis ad determinandas positiones imaginis et obiecti in lentibus tenuibus.
• Computare magnificationem imaginum a lentibus tenuibus productarum.
• Deducere formulas ex geometria lentium tenuium ad problemata optica solvenda.

INDEX CONTENTORUM
Introductio
Genera lentium
Proprietates lentium tenuium
Aequatio fabricantium lentium
Methodi graphici pro lentibus tenuibus
Exercitia

Introductio

Lentes tenues, una cum speculis, sunt longe frequentissime adhibita instrumenta optica. Haec sunt corpora transparens quorum superficies duabus interfaciebus sphaericis terminatur et plerumque ex vitro vel plastico fiunt.

In lente tenui, distantia inter superficies refractivas tam exigua est ut neglegenda habeatur.

Genera lentium

Lentes, sicut et specula, in duas species dividuntur: convergentes et divergentes.

 

Puncta F_1 et F_2 sunt puncta focalia et f est distantia focalis. In lente tenui, duae longitudines focales aequales sunt, ideo utraque eadem littera repraesentatur.

In lente tenui, distantia inter superficies refractivas tam exigua est ut neglegenda habeatur.

Proprietates lentium tenuium

Si geometriam cum lente convergente facimus, sequentia videbimus:

 

Cum triangula depicta similia sint, erit ut latera correspondentia proportionalia sint

\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}

Similiter

\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}

Deinde, ex (\triangle) et (\star) habetur:

\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}

Hoc ultimum est quod appellamus relationem obiecti-imaginis pro lentibus tenuibus.

Simili modo ac in speculis laboratur, fieri potest definire factor magnificationis m per

\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}

Aequatio fabricantium lentium

Lens tenuis, ut scimus, ex duabus interfaciebus sphaericis constat quae media distinguunt per quae lux propagatur, et iam perspeximus quid accidat cum lux e medio in aliud medium per huiusmodi interfacies transeat. Itaque, ad lentes tenues perpendendas sufficiet componere quod iam de singulis interfaciebus consideravimus.

In universum, lens tenuis hanc speciem habet:

Sed ad maiorem simplicitatem, hoc separari potest

Cum unumquodque casum iam perscrutati simus (hic), possumus sequentia duo aequationes deducere:

Pro latere a-b:

\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}

Pro latere b-c:

\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}

Hoc loco, si ponimus n_a = n_c = n_{aer}\approx 1.0, eveniet s_b = -s_{ab}^\prime; itaque hae aequationes ita scribuntur

\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}

et eas addendo, nunc fieri potest unam expressionem obtinere:

\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}

Hoc loco expedit variabiles mutare; adhibebimus hanc substitutionem

\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}

ita ut versionem magis “puram” aequationis quam initio invenimus obtineamus:

\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)

Denique, utens relatione obiecti-imaginis pro lentibus tenuibus initio deducta, obtinetur:

\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}

Hoc est quod appellamus Aequationem Fabricantium Lentium.

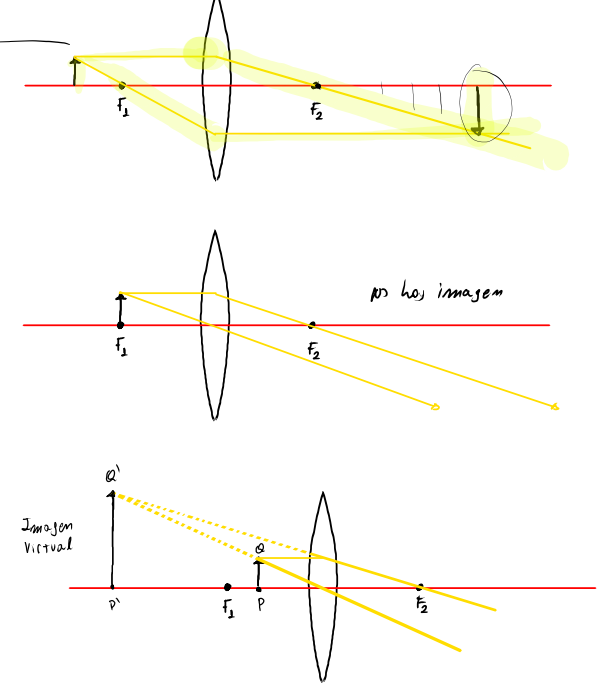
Methodi graphici pro lentibus tenuibus

Instrumentum valde utile ad confirmandum vel ad sensum inveniendum calculorum quos fecimus sunt methodi graphici infra depicti; tales methodi analogi sunt iis qui cum speculis adhibentur.

Hi methodi diversos exitus praebent secundum situm obiecti coram lente.

Exercitia:

1. Habemus lentem divergentem et fasciculum radiorum parallelorum qui “aperitur” transeundo per eam ita ut projectiones eius ad punctum 30[cm] a centro lentis situm confluant. Si haec lens adhiberi velit ad imaginem virtualem obtinendam cuius altitudo est dimidia altitudinis cuiusdam obiecti:
   1. Computa locum ubi tale obiectum poni debeat.
   2. Fac diagramma radiorum ad describendam condicionem.
2. Obiectum 7[cm] altitudinis ponitur 13[cm] ad sinistram lentis convergentis longitudinis focalis 5[cm]. Secunda lens convergens longitudinis focalis 2[cm] ponitur 30[cm] ad dextram primae lentis, eundem axem opticorum communicantes. Inveni magnitudinem et situm imaginis a duabus lentibus coniunctis generatae.