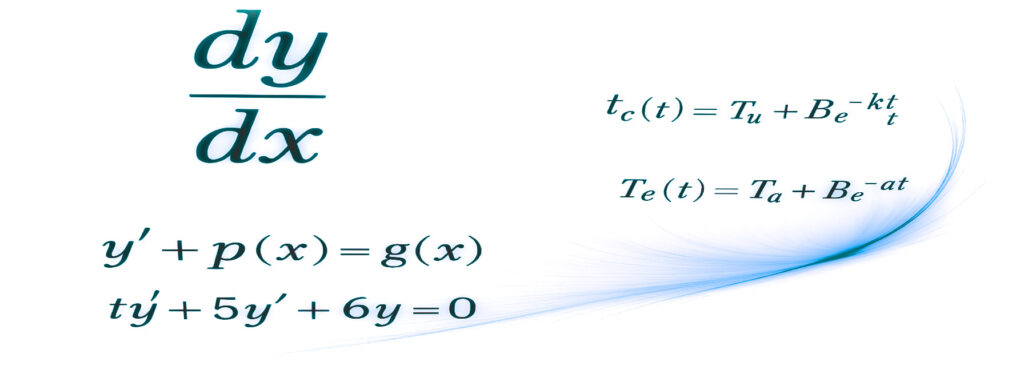साधारण अवकल समीकरणों का परिचय
इस कक्षा में इन समीकरणों और विभिन्न क्षेत्रों में उनके अनुप्रयोगों को नियंत्रित करने वाले मौलिक विचारों की विस्तृत खोज की जाती है। हमारे चारों ओर की दुनिया में निरंतर परिवर्तन की प्रकृति के विश्लेषण से शुरू होकर, कार्य, अवकलज और निरंतर तथा विविक्त परिवर्तन के साथ उनके संबंध जैसे मूलभूत अवधारणाओं को प्रस्तुत किया जाता है। आंशिक अवकल समीकरणों (ईडीपी) और साधारण अवकल समीकरणों (ईडीओ) के बीच के अंतर को प्रस्तुत किया जाता है, जिसमें ईडीओ के अध्ययन पर ध्यान केंद्रित किया गया है। व्यावहारिक उदाहरणों जैसे एक कप कॉफी का ठंडा होना, न्यूटन के नियम और जनसंख्या मॉडल के माध्यम से अवधारणाओं को स्पष्ट किया जाता है। छात्रों को प्राकृतिक और भौतिक घटनाओं को नियंत्रित करने वाले अवकल समीकरणों से परिचित होने, उन्हें गणितीय रूप से कैसे दर्शाया जा सकता है यह जानने और उनके समाधानों का अध्ययन करने की कुछ तकनीकों को समझने का अवसर मिलेगा। यह प्रारंभिक ज्ञान अवकल समीकरणों और विज्ञान एवं अभियांत्रिकी में उनके अनुप्रयोगों के उन्नत अध्ययन के लिए आधार तैयार करेगा।
अध्ययन के उद्देश्य:
इस कक्षा के अंत में छात्र सक्षम होगा:
- समझना अवकल समीकरणों से संबंधित मूलभूत अवधारणाओं को, जैसे परिवर्तन की प्रकृति, कार्य, अवकलज और आंशिक (ईडीपी) और साधारण (ईडीओ) अवकल समीकरणों के बीच का अंतर
सूचकांक
अवकल समीकरण और वस्तुओं की प्रकृति
निरंतर परिवर्तन
कार्य, अवकलज और उनके परिवर्तन
ईडीओ और ईडीपी
साधारण अवकल समीकरणों के उदाहरण
एक कप कॉफी का ठंडा होना
न्यूटन के नियम
जनसंख्या मॉडल
अवकल समीकरण और वस्तुओं की प्रकृति
निरंतर परिवर्तन
प्रकृति में, सब कुछ निरंतर परिवर्तन में है। यहाँ तक कि जो कुछ कभी नहीं बदलता प्रतीत होता है, जैसे सूर्य की चमक, वह भी समय के उपयुक्त पैमाने पर देखने पर बदलती है। सब कुछ बदलता है: तारों की चमक, एक कप में कॉफी का तापमान, किसी वस्तु की स्थिति, और किसी जनसंख्या का आकार कुछ उदाहरण हैं, और इन परिवर्तनों की दरें आमतौर पर उस वस्तु की अवस्था से जुड़ी होती हैं जो परिवर्तन के दौरान बदल रही होती है।
परिवर्तन को समझने का एक सहज तरीका है यह देखना कि समय बीतने के साथ चीजें कैसे बदलती हैं। जो परिवर्तन समय के सापेक्ष होता है, उसे हम विकास (evolution) कहते हैं, और जो कुछ भी हम देख सकते हैं वह निरंतर विकासशील है। लेकिन विकास परिवर्तन का एकमात्र रूप नहीं है; उदाहरण के लिए, यद्यपि समुद्र तल से हमारी ऊँचाई समय के साथ बदल सकती है, यह अधिक संभावित है कि यह हमारी स्थिति (या भौगोलिक निर्देशांकों) के अनुसार बदले।
कार्य, अवकलज और उनके परिवर्तन
और अधिक सामान्य शब्दों में, कई चरों वाला एक फलन f(x_1,x_2, \cdots, x_n) तब बदल सकता है जब इसकी कोई भी चर बदले, और यह परिवर्तन सतत या विविक्त हो सकता है। कई चरों वाले फलन के लिए, सतत परिवर्तन का अध्ययन आंशिक अवकलज के माध्यम से किया जा सकता है:
\displaystyle \frac{\partial f(x_1, \cdots, x_n)}{\partial x_1} = \lim_{\Delta x_1 \to 0} \frac{ f(x_1 + \Delta x_1, \cdots, x_n) - f(x_1, \cdots, x_n)}{\Delta x_1}
यदि फलन एक ही चर पर निर्भर करता है, तो साधारण अवकलज का प्रयोग किया जाता है:
\displaystyle \frac{df(x)}{dx} = \lim_{\Delta x \to 0} \frac{ f(x + \Delta x) - f(x)}{\Delta x}
यदि परिवर्तन सतत के बजाय विविक्त हो, तो अवकलज में दिखाई देने वाली सीमा (limit) की गणना नहीं की जाती।
ईडीओ और ईडीपी
एक समीकरण जिसमें किसी फलन और उसके विभिन्न अवकलज शामिल हों उसे अवकल समीकरण कहा जाता है। यदि ये अवकलज आंशिक या साधारण हों, तो इन्हें क्रमशः आंशिक अवकल समीकरण (ईडीपी) या साधारण अवकल समीकरण (ईडीओ) कहा जाता है। इस समय, हम साधारण अवकल समीकरणों के अध्ययन पर ध्यान केंद्रित करेंगे और कुछ उदाहरणों की समीक्षा करेंगे जहाँ ये दिखाई देते हैं।
साधारण अवकल समीकरणों के उदाहरण
एक कप कॉफी का ठंडा होना
एक कप कॉफी के ठंडा होने की दर वातावरण और कॉफी के तापमान के अंतर के अनुपात में होती है। यदि हवा का तापमान T_a स्थिर है और कॉफी का तापमान समय का फलन है T_c=T_c(t), तो हम एक अवकल समीकरण प्राप्त कर सकते हैं जो हमें प्रत्येक क्षण में कॉफी का तापमान निर्धारित करने की अनुमति देगा। प्रारंभ में हमारे पास होता है:
\displaystyle \frac{dT_c(t)}{dt} = -\alpha^2(T_c(t) - T_a)
जहाँ \alpha एक अनुपातांक (proportionality constant) है, T_a \lt T_c(t) और ऋणात्मक चिन्ह दर्शाता है कि कॉफी का तापमान घट रहा है। बाद में, हम देखेंगे कि इस समीकरण का हल इस रूप में होता है:
T_c(t) = T_a + Be^{-\alpha^2 t}
जहाँ B एक नियतांक (constant) है जिसे निर्धारित किया जाना है।
न्यूटन के नियम
न्यूटन का द्वितीय नियम मूल रूप से एक साधारण अवकल समीकरण है, क्योंकि अभिव्यक्ति F=ma (बल = द्रव्यमान × त्वरण) में, त्वरण a=d^2x(t)/dt^2, वस्तु की स्थिति का समय के सापेक्ष द्वितीय अवकलज है। इस नियम के माध्यम से, हम ऐसे संबंध प्राप्त कर सकते हैं जो पिंडों की गति का वर्णन करते हैं, जो वास्तव में अवकल समीकरण होते हैं। एक सरल उदाहरण है स्प्रिंग का अध्ययन: यदि हमारे पास एक स्प्रिंग है जो एक ओर एक दीवार से और दूसरी ओर एक द्रव्यमान से जुड़ा हुआ है, और हम उस द्रव्यमान को संतुलन की स्थिति से x दूरी तक विस्थापित करते हैं, तो हुक के नियम के अनुसार उस द्रव्यमान पर प्रत्यास्थ बल F=-kx कार्य करेगा। फिर न्यूटन के द्वितीय नियम के अनुसार, हमें प्राप्त होता है:
\displaystyle -kx(t) = m\frac{d^2x(t)}{dt^2}
आगे हम देखेंगे कि इसका समाधान इस रूप में होता है:
\displaystyle x(t) = A\sin\left(\sqrt{\frac{k}{m}}t + \phi \right)
जहाँ A और \phi नियतांक हैं जिन्हें समस्या की प्रारंभिक स्थितियों द्वारा निर्धारित किया जाएगा।
जनसंख्या मॉडल
प्रति व्यक्ति वृद्धि दर किसी जनसंख्या की जन्म और मृत्यु दर के बीच अंतर के बराबर होती है, अर्थात्:
\displaystyle \frac{1}{x(t)} \frac{dx(t)}{dt} = N - M
यदि जन्म दर N समय के साथ स्थिर रहती है और मृत्यु दर जनसंख्या के समानुपाती हो, अर्थात् M=\alpha^2 x(t), तब उपरोक्त समीकरण इस रूप में परिवर्तित हो जाता है:
\displaystyle \frac{dx(t)}{dt} = x(t) (N - \alpha^2 x(t))
इसे “जनसंख्या की लॉजिस्टिक समीकरण” के रूप में जाना जाता है। इस समीकरण से, हम कई जनसंख्याओं x_1(t), x_2(t), \cdots, x_n(t) के लिए एक सामान्यीकरण बना सकते हैं जो अस्तित्व के लिए आपस में प्रतिस्पर्धा करती हैं:
\displaystyle \frac{dx_i(t)}{dt} = x_i(t) \left(N_i - \displaystyle \sum_{j=1}^n\alpha^2_{ij} x_j(t) \right)
जहाँ i\in\{1,\cdots, n\}। इसे लॉटका-वोल्टेरा समीकरण के नाम से जाना जाता है।
निष्कर्ष
साधारण अवकल समीकरणों के इस परिचय के दौरान, हमने देखा कि कैसे गणित प्राकृतिक जगत में होने वाले परिवर्तनों को सटीक और सुरुचिपूर्ण ढंग से दर्शा सकता है। चाहे वह एक कप कॉफी का ठंडा होना हो, एक स्प्रिंग की गति या जनसंख्या की वृद्धि — ईडीओ हमें जटिल गतिशीलताओं को समझने योग्य गणितीय संबंधों में अनुवाद करने की अनुमति देते हैं।
इन समीकरणों की संरचना और अर्थ को समझना भौतिकी, जीवविज्ञान, अर्थशास्त्र और अभियांत्रिकी जैसी कई विधाओं के लिए मार्ग खोलता है। यह कक्षा उन वैचारिक नींवों की स्थापना करती है जो आगे के उन्नत अध्ययन — जैसे समाधान तकनीकें, गुणात्मक विश्लेषण और संख्यात्मक विधियाँ — के लिए आवश्यक हैं। हालांकि, सबसे महत्वपूर्ण बात यह है कि हमने परिवर्तन की भाषा — अवकल समीकरणों — के माध्यम से गतिशील प्रणालियों के व्यवहार को वर्णित, समझने और पूर्वानुमान लगाने की प्रारंभिक अंतर्दृष्टि विकसित की है।
आगामी कक्षाओं में हम और अधिक शक्तिशाली उपकरणों को विकसित करते रहेंगे और उन्हें नए संदर्भों में लागू करेंगे। अवकल समीकरण न केवल वास्तविकता का विश्लेषण करने का एक साधन हैं, बल्कि यह कल्पना करने का भी एक माध्यम हैं कि विभिन्न परिस्थितियों में चीजें कैसे विकसित हो सकती हैं।