पतली लेंस: उनकी विशेषताओं और गणनाओं के बारे में सब कुछ
सारांश:
यह कक्षा पतली लेंस की परिचय देती है, उनके प्रकार (अभिसारी और अपवर्तक), उनकी ऑप्टिकल विशेषताओं और वस्तु-छवि संबंध की व्याख्या करती है। ग्राफिकल विधियों को प्रस्तुत किया गया है, और लेंस निर्माता समीकरण को उनके कार्य करने के तरीके को समझने के लिए व्युत्पन्न किया गया है। उद्देश्य यह है कि पतली लेंस और ऑप्टिक्स में उनके अनुप्रयोग के बारे में बुनियादी समझ प्रदान की जाए, जिसे व्यावहारिक अभ्यास के साथ पूरा किया गया है।
अध्ययन के उद्देश्य:
इस कक्षा के अंत तक, छात्र सक्षम होंगे:
- समझना पतली लेंस की ऑप्टिकल विशेषताओं को, जिसमें फोकल लंबाई और फोकल पॉइंट शामिल हैं।
- पहचानना पतली लेंस के विभिन्न प्रकार, जैसे कि अभिसारी और अपवर्तक लेंस और उनके अनुप्रयोग।
- लागू करना वस्तु-छवि संबंध को पतली लेंस का उपयोग करके ऑप्टिकल समस्याओं को हल करने के लिए।
- विश्लेषण करना कि कैसे पतली लेंस में गोलाकार सतहें प्रकाश के अपवर्तन को प्रभावित करती हैं।
- समझाना लेंस निर्माता समीकरण और ऑप्टिकल लेंस के निर्माण में इसकी प्रासंगिकता।
- उपयोग करना ग्राफिकल विधियों को पतली लेंस में वस्तु और छवि की स्थिति निर्धारित करने के लिए।
- गणना करना पतली लेंस द्वारा उत्पादित छवियों की आवर्धन।
- व्युत्पन्न करना पतली लेंस के ज्यामिति से सूत्रों का उपयोग करके ऑप्टिकल समस्याओं को हल करना।
विषय-सूची
परिचय
लेंस के प्रकार
पतली लेंस की विशेषताएं
लेंस निर्माता समीकरण
पतली लेंस के लिए ग्राफिकल विधियाँ
अभ्यास
परिचय
पतली लेंस, दर्पणों के साथ, सबसे अधिक उपयोग किए जाने वाले ऑप्टिकल उपकरण हैं। ये पारदर्शी वस्तुएं हैं जिनकी सतह दो गोलाकार इंटरफेस द्वारा सीमित होती हैं और ये आमतौर पर कांच या प्लास्टिक से बनी होती हैं।

एक पतली लेंस में, अपवर्तक सतहों के बीच की दूरी इतनी छोटी होती है कि उसे नगण्य माना जा सकता है।
लेंस के प्रकार
लेंस, दर्पणों की तरह, दो प्रकारों में विभाजित किए जाते हैं: अभिसारी और अपवर्तक।
 पतली अभिसारी लेंस
पतली अभिसारी लेंस  पतली अपवर्तक लेंस
पतली अपवर्तक लेंस
बिंदु F_1 और F_2 फोकल पॉइंट हैं, और f है फोकल लंबाई। एक पतली लेंस में, दोनों फोकल लंबाइयां समान होती हैं, इसलिए उन्हें एक ही अक्षर से दर्शाया जाता है।
एक पतली लेंस में, अपवर्तक सतहों के बीच की दूरी इतनी छोटी होती है कि उसे नगण्य माना जा सकता है।
पतली लेंस की विशेषताएं
अगर हम एक अभिसारी लेंस के साथ ज्यामिति करते हैं, तो हम निम्नलिखित देखेंगे:

चूंकि खींचे गए त्रिभुज समान होते हैं, संबंधित पक्ष अनुपात में होंगे
\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}
इसी तरह,
\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}
फिर, (\triangle) और (\star) से हमें मिलता है:
\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}
उपरोक्त वह है जिसे हम पतली लेंस के लिए वस्तु-छवि संबंध कहते हैं।
वृद्धि कारक m को परिभाषित करना संभव है
\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}
लेंस निर्माता समीकरण
एक पतली लेंस, जैसा कि हम जानते हैं, दो गोलाकार इंटरफेस से बनी होती है जो माध्यमों को अलग करती हैं जिनके माध्यम से प्रकाश यात्रा करता है, और हमने पहले ही अध्ययन किया है कि जब प्रकाश एक माध्यम से दूसरे माध्यम में प्रवेश करता है तो क्या होता है। इसलिए, पतली लेंस का विश्लेषण करने के लिए, हमें केवल व्यक्तिगत इंटरफेस के लिए पहले से अध्ययन किए गए ज्ञान को जोड़ना होगा।
सामान्य तौर पर, पतली लेंस निम्नलिखित उपस्थिति रखती है:

लेकिन सरलता के लिए, इसे अलग किया जा सकता है

चूंकि हमने पहले ही हर मामले का विश्लेषण किया है (यहां), हम निम्नलिखित दो समीकरण निकाल सकते हैं:
पक्ष a-b के लिए:
\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}
पक्ष b-c के लिए:
\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}
इस बिंदु पर, यदि हम n_a = n_c = n_{air}\approx 1.0, स्थापित करते हैं, तो s_b = -s_{ab}^\prime; परिणामस्वरूप, ये समीकरण निम्नलिखित रूप में लिखे जाएंगे
\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}
और उन्हें जोड़ने से, अब एक ही अभिव्यक्ति प्राप्त करना संभव है:
\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}
इस बिंदु पर, शामिल किए गए चर का पुन: नामकरण करना सुविधाजनक है; हम निम्नलिखित नाम परिवर्तन का उपयोग करेंगे
\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}
इस प्रकार, हम समीकरण के एक “स्वच्छ” संस्करण को प्राप्त करेंगे जिसे हमने मूल रूप से प्राप्त किया था:
\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)
अंत में, पतली लेंस के लिए वस्तु-छवि संबंध का उपयोग करके जो शुरू में व्युत्पन्न किया गया था, हम प्राप्त करते हैं:
\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}
यह वह है जिसे हम लेंस निर्माता समीकरण कहते हैं।
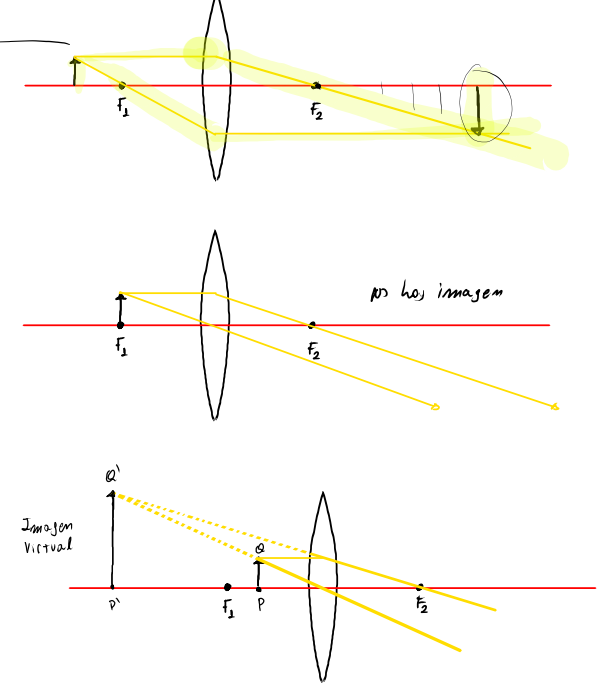
पतली लेंस के लिए ग्राफिकल विधियाँ
उनकी गणना को सत्यापित करने के लिए या समझने के लिए एक बहुत उपयोगी उपकरण नीचे खींची गई ग्राफिकल विधियाँ हैं; ये विधियाँ दर्पणों के साथ उपयोग की जाने वाली विधियों के अनुरूप हैं।

ये विधियाँ वस्तु के लेंस के सामने की स्थिति के आधार पर अलग-अलग परिणाम देती हैं।
अभ्यास:
- हमारे पास एक अपवर्तक लेंस और एक समांतर किरणों का बंडल है जो लेंस के माध्यम से गुजरते समय “खुलता” है ताकि उनके प्रक्षेपण एक बिंदु पर अभिसरण करें जो लेंस के केंद्र से 30[सेमी] दूर स्थित है। यदि आप इस लेंस का उपयोग करना चाहते हैं ताकि एक वस्तु की ऊंचाई का आधा वर्चुअल इमेज प्राप्त हो सके:
- उस वस्तु को कहां रखा जाना चाहिए, इसका गणना करें।
- इस स्थिति का वर्णन करने के लिए एक किरण आरेख बनाएं।
- 7[सेमी] ऊंचाई वाली वस्तु को 13[सेमी] दूर एक अभिसारी लेंस के बाईं ओर रखा गया है जिसकी फोकल लंबाई 5[सेमी] है। दूसरी अभिसारी लेंस, जिसकी फोकल लंबाई 2[सेमी] है, पहले लेंस के दाईं ओर 30[सेमी] की दूरी पर रखा गया है, दोनों एक ही ऑप्टिकल अक्ष को साझा कर रहे हैं। इन दोनों लेंसों के संयोजन द्वारा उत्पन्न छवि का आकार और स्थिति ज्ञात करें।

