المقدمة

العدسات الرقيقة، إلى جانب المرايا، هي إلى حد بعيد أكثر الأجهزة البصرية استخدامًا. هذه هي الأشياء الشفافة التي تحدها واجهتان كرويتان وعادة ما تكون مصنوعة من الزجاج أو البلاستيك.

في العدسة الرقيقة، تكون المسافة بين الأسطح الانكسارية صغيرة بما يكفي لتعتبر مهملة.

أنواع العدسات

العدسات، مثل المرايا، تنقسم إلى نوعين: مجمعة ومفرقة.

النقاط F_1 و F_2 هي النقاط البؤرية، و f هو البعد البؤري. في العدسة الرقيقة، تكون البعدين البؤريين متساويين، لذا يتم تمثيلهما بنفس الحرف.

في العدسة الرقيقة، تكون المسافة بين الأسطح الانكسارية صغيرة بما يكفي لتعتبر مهملة.

خصائص العدسات الرقيقة

إذا قمنا بتحليل هندسي بعدسة مجمعة، سنرى ما يلي:

بما أن المثلثات المرسومة متشابهة، فإن الأضلاع المقابلة ستكون متناسبة

\begin{array}{rlr} &\displaystyle \frac{y}{s} = -\frac{y^\prime}{s^\prime} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime}{s}} & (\triangle) \end{array}

وبالمثل،

\begin{array}{rlr} & \displaystyle \frac{y}{f} = -\frac{y^\prime}{s^\prime-f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{y^\prime}{y} = -\frac{s^\prime-f}{f}} & (\star) \end{array}

ثم، من (\triangle) و (\star) نحصل على:

\begin{array}{rlr} &\displaystyle-\frac{s^\prime}{s} = -\frac{s^\prime-f}{f} & \\ \\ \equiv \displaystyle & \frac{s^\prime}{s} = \frac{s^\prime-f}{f} = \frac{s^\prime}{f} - 1 = \frac{s^\prime}{f} - \frac{s^\prime}{s^\prime} & \\ \\ {} \equiv & \displaystyle \frac{s^\prime}{s}+ \frac{s^\prime}{s^\prime} = \frac{s^\prime}{f} & \\ \\ \equiv & \displaystyle \color{blue}{\frac{1}{s}+ \frac{1}{s^\prime} = \frac{1}{f}} & \end{array}

هذا هو ما نسميه علاقة الجسم-الصورة للعدسات الرقيقة.

عامل التكبير m من خلال

\displaystyle \color{blue}{m=-\frac{y^\prime}{y}= - \frac{s^\prime}{s}}

معادلة صانع العدسات

نعلم أن العدسة الرقيقة تتكون من واجهتين كرويتين تفصلان الوسطين اللذين تنتقل من خلالهما الضوء، وقد درسنا بالفعل ما يحدث عندما يمر الضوء من وسط إلى آخر عبر هذه الواجهات. لذا، لتحليل العدسات الرقيقة، يكفي أن ندمج ما درسناه سابقاً للواجهات الفردية.

بوجه عام، العدسة الرقيقة لها الشكل التالي:

ولكن لتبسيط الأمور، يمكن فصلها

نظرًا لأننا قد حللنا بالفعل كل حالة (هنا)، يمكننا استخراج المعادلتين التاليتين:

لجانب a-b:

\displaystyle \frac{n_a}{s_a} + \frac{n_b}{s_{ab}^\prime} = \frac{n_b - n_a}{R_c}

لجانب b-c:

\displaystyle \frac{n_b}{s_{b}} + \frac{n_c}{s_{bc}^\prime} = \frac{n_c - n_b}{R_a}

في هذه المرحلة، إذا قمنا بتعيين n_a = n_c = n_{air}\approx 1.0, سيحدث أن s_b = -s_{ab}^\prime; لذلك، تتم كتابة هذه المعادلات على النحو التالي

\begin{array}{rl} \displaystyle \frac{1}{s_a} + \frac{n_b}{s_{ab}^\prime} & \displaystyle = \frac{n_b - 1}{R_c} \\ \\ \displaystyle -\frac{n_b}{s_{ab}^\prime} + \frac{1}{s_{bc}^\prime} & \displaystyle= \frac{1-n_b}{R_a} \end{array}

وبجمعهما، يمكننا الآن الحصول على تعبير واحد:

\begin{array}{rl} &\displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = \frac{n_b-1}{R_c} + \frac{1-n_b}{R_a} \\ \\ \equiv & \displaystyle \frac{1}{s_a} + \frac{1}{s_{bc}^\prime} = (n_b -1) \left( \frac{1}{R_a} - \frac{1}{R_c} \right) \end{array}

في هذه المرحلة، من المناسب إعادة تسمية المتغيرات المعنية؛ سنستخدم التسمية التالية

\begin{array}{ll} s_a = s & R_a = R_1 \\ \\ s_{bc}^\prime = s^\prime & R_c =R_2 \\ \\ n_b =n & \end{array}

وبالتالي، سنحصل على نسخة “أنظف” من المعادلة التي حصلنا عليها في الأصل:

\displaystyle \frac{1}{s} + \frac{1}{s^\prime} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)

أخيرًا، باستخدام علاقة الجسم-الصورة للعدسات الرقيقة التي تم استنتاجها في البداية، نحصل على:

\displaystyle \color{blue}{\frac{1}{f} = (n -1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)}

هذا ما نسميه معادلة صانع العدسات.

الأساليب البيانية للعدسات الرقيقة

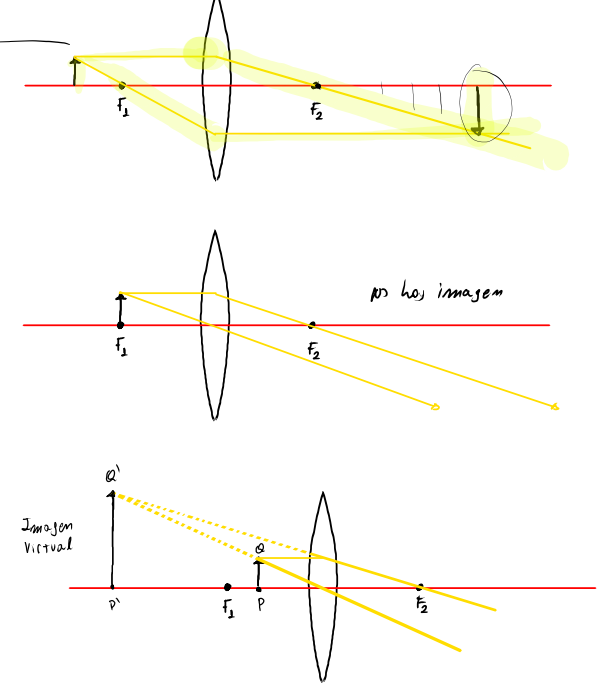
أداة مفيدة للغاية للتحقق من أو فهم الحسابات التي نقوم بها هي الأساليب البيانية الموضحة أدناه؛ هذه الأساليب مشابهة لتلك المستخدمة مع المرايا.

تقدم هذه الأساليب نتائج مختلفة حسب موقع الجسم أمام العدسة.

التمارين:

1. لدينا عدسة مفرقة وحزمة من الأشعة المتوازية “تتفتح” عند مرورها عبرها بحيث تتقارب إسقاطاتها إلى نقطة تقع على بعد 30[سم] من مركز العدسة. إذا كنت ترغب في استخدام هذه العدسة للحصول على صورة افتراضية نصف ارتفاعها من ارتفاع جسم معين:
   1. احسب المكان الذي يجب أن يكون فيه هذا الجسم.
   2. قم بعمل رسم بياني للأشعة لوصف الموقف.
2. تم وضع جسم بارتفاع 7[سم] على مسافة 13[سم] إلى يسار عدسة مجمعة ببعد بؤري 5[سم]. تم وضع عدسة مجمعة ثانية ببعد بؤري 2[سم] على مسافة 30[سم] إلى يمين العدسة الأولى بحيث تتشارك كلا العدستين في نفس المحور البصري. حدد حجم وموقع الصورة التي تنتجها العدستان المجمعتان معًا.